留数

字数统计: 3.6k阅读时长: 20 min

 2020/06/23   Share

留数

5. 留数

5. 留数5.1 孤立奇点5.2 留數5.3 留数在定积分计算中的应用5.4 复变函数奇点类型的判定

首先说明一下为什么会有留数？

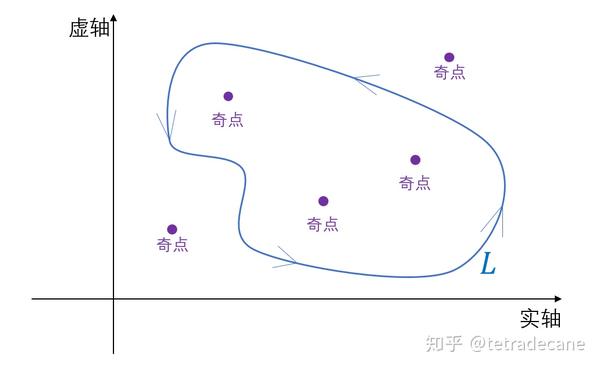
对于图中的这样一个积分路径，由于内部区域不完全解析。所以根据柯西积分定理，我们可以将其转化为下图的积分路径：

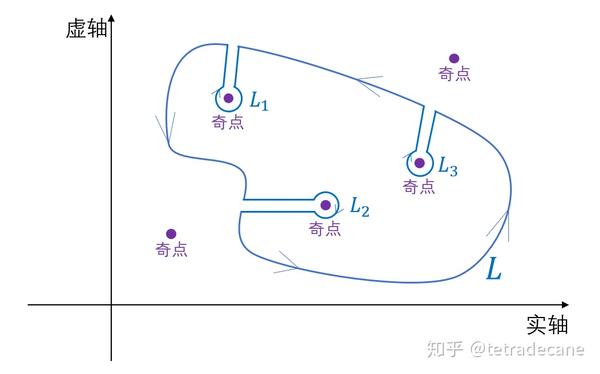
当通往奇点的两条路线无限接近时，就可以得到下图：

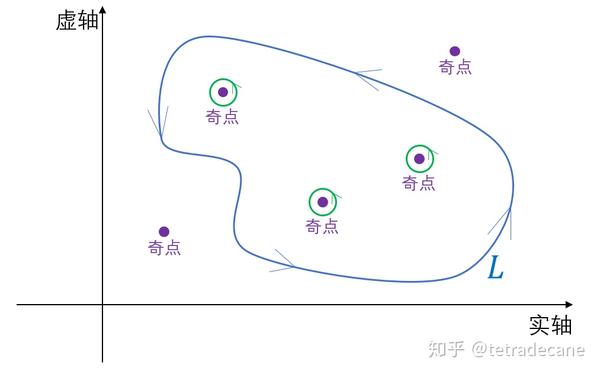
即对于大回路的积分等于对所有奇点的路径的积分之和的相反数。即：

\oint_L = \oint_{L_1^-+L_2^-+L_3^-}

$\oint_Lf(z)dz$

由上一章的洛朗级数知，洛朗级数在幂次为-1项的系数为

c_{-1} = \frac1{2\pi i}\oint_C\frac{f(\zeta)}{(\zeta-z_0)^{-1+1}}d\zeta = \frac1{2\pi i}\oint_Cf(\zeta)d\zeta

留数 $\mathcal{Res}[f(z),z_0]$

$z_1,z_2,\cdots,z_k$ 外处处解析，则有

\oint_Cf(z)dz = 2\pi i\sum_{k=1}^n\mathcal{Res}[f(z),z_k]

所以留数定理本质上是对于柯西积分定理的应用。

5.1 孤立奇点

5.1.1 解析函数的孤立奇点及分类

$z_0$ $z_0$ $z_0$ 为f(z)的一个孤立奇点。

根据洛朗级数的定理，我们可以将f(z)展开成洛朗级数

f(z) =\cdots+ a_{-m}(z-z_0)^{-m} + \cdots+ a_0 + a_1(z-z_0) + \cdots + a_n(z-z_0)^n,z\in D

$z_0$ $z\in D$ $z=z_0$ $F(z) = a_0$ $f(z_0) = a_0$ $z_0$ $z_0$ 被称为可去奇点。
$(z-z_0)$ $z_0$ 极点 $(z-z_0)^{-m}$ $z_0$ 为函数f(z)的m阶极点。
$(z-z_0)$ $z_0$ 称之为f(z)的本性奇点。

5.1.2 解析函数在有限孤立奇点的性质

定理： $0<|z-z_0|<\delta$ $z_0$ 可去奇点 $\lim_{z\rightarrow z_0}f(z)$ .

定理： $0<|z-z_0|<\delta$ $z_0$ 极点 $\lim_{z\rightarrow z_0}f(z) = \infty$ .

定理 $0<|z-z_0|<\delta$ $z_0$ 本性奇点 $\lim_{z\rightarrow z_0}f(z)$ .

$e^{\frac1z}$ 在z=0处为本性奇点，因为其展开成洛朗级数后有无穷多个负幂项不为0

5.1.3 函数的零点与极点的关系

$z_0$ $N(z_0,\delta)=\{z:|z-z_0|<\delta \}$ $f(z_0)=0$ $z_0$ 称为f(z)的一个零点。

m阶零点

$f(z) = (z-z_0)^m\varphi(z)$ $\varphi(z)$ $z_0$ $\varphi(z)\ne 0$ $z_0$ 为f(z)的m级零点。

定理 $z_0$ $z_0$ $f(z_0) = f^{'}(z_0) = f^{(m-1)}(z_0) = 0,f^{m}(z_0)\ne 0$

解析函数的零点与极点，有下面的关系

定理： $z_0$ $z_0$ $\frac1{f(z)}$ 的m阶零点。

$(\cos z-1)/z^4$ ，看起来z=0是它的四阶奇点，实际将cos z展开后是二阶奇点。

$f(z) = \frac{\sin z}{z^2(1-e^z)}$ $z=0$ 是几阶极点。

$1-e^z$ $\sin z$ 展开

5.1.4 解析函数在无穷孤立奇点的性质

$R<|z|<+\infty(R>0)$ $z=\infty$ 为f(z)的一个孤立奇点。

5.2 留數

5.2.1 留數的定义和计算规则

定义： $z_0$ $z_0$ $z_0$ 的留数定义为

\frac1{2\pi i}\oint_Cf(z)dz

$Res[f(z),z_0]$ $z_0$ 的任何一条正向简单闭曲线。留数的本质还是一个柯西积分。

$z=\infty$ $z=\infty$ 处的留数为

Res[f(z),\infty] = -\frac1{2\pi i}\oint_Cf(z)dz

留数的计算定理 $z_0$ 是f(z)的m阶极点，则

Res[f(z),z_0] = \frac1{(m-1)!}\lim_{z\rightarrow z_0}\frac{d^{m-1}}{dz^{m-1}}\{(z-z_0)^mf(z) \}

$a_{-1}$

推论 $f(z) = P(z)/Q(z)$ $P(z)$ $Q(z)$ $z_0\in C$ $P(z_0)\ne 0,Q(z_0)=0,Q'(z)\ne0$ $z_0$ $f(z)$ 的一阶极点，且

\mathcal{Res}[f(z),z_0] = \frac{P(z_0)}{Q'(z_0)}

$z_0$ $f(z)$ $\mathcal{Res}[f(z),z_0] = a_{-1}$ 。

$z=\infty$ $f(z)$ 的孤立奇点，则

Res[f(z),\infty] = -Res[f(\frac1z)\frac1{z^2}, 0]

5.2.2 留数的基本定理

$z_1,z_2,\cdots,z_k$ 外处处解析，则有

\oint_Cf(z)dz = 2\pi i\sum_{k=1}^n\mathcal{Res}[f(z),z_k]

推广的留数基本定理 $\infty$ 点）的留数之和等于0。

利用该定理，当所求留数的区域内有多个极点时，可以直接求无穷远处的留数值，则其他点的留数之和就等于无穷远的留数值之和。

5.3 留数在定积分计算中的应用

$\overline D$ 上对F(z)应用留数定理，就能把实轴上f(x)的积分转换为F(z)在D内基地那的留数与附加曲线的积分。

$\int_0^{2\pi}R(\sin\theta,\cos\theta)d\theta$ 的积分

$z = e^{i\theta}$ ，则

\cos\theta = \frac{e^{i\theta} + e^{-i\theta}}2 = \frac12(z+\frac1z)\\ \sin\theta = \frac1{2i}(z-\frac1z)\\ d\theta = \frac1{iz}dz

于是

\int_0^{2\pi}R(\sin\theta,\cos\theta)d\theta = \oint_{|z|=1}R(\frac1{2i}(z-\frac1z),\frac1{2}(z+\frac1z))\frac1{iz}dz

令

F(z) = \frac1{iz}R[\frac1{2i}(z-\frac1z),\frac12(z+\frac1z)]

则由留数的基本定理知

\int_0^{2\pi}R(\sin\theta,\cos\theta)d\theta = 2\pi i\sum^n_{k=1}Res[F(z),a_k]

$\int_{-\infty}^{+\infty}R(x)dx$ 的积分

当被积函数R(x)是x的有理函数高二次 $Im\ z>0$ $a_1,a_2,\cdots,a_p$ ，则

\int_{-\infty}^{+\infty}R(x)dx = 2\pi i\sum_{k=1}^p\mathcal{Res}[R(z),a_k]

证明过程略

$R(x)$ 为偶函数时，有

\int_0^{+\infty}R(x)dx = \pi i\sum_{k=1}^p\mathcal{Res}[R(z),a_k]

注意只考虑上半平面的极点。

$\int_{-\infty}^{+\infty}R(x)e^{iax}dx$ 的积分

当被积函数R(x)是x的有理函数，而分母次数至少比分子的高一次，并且R(x)在实轴上没有奇点上半平面 $a_1,a_2.\cdots,a_p$ ，则

\int_{-\infty}^{+\infty}R(x)e^{iax}dx = 2\pi i\sum_{k=1}^p\mathcal{Res}[R(z)e^{iaz},a_k]

证明过程略。

5.3.4 它类

在前几类积分中，都要求函数在实轴上无奇点，对不满足这个条件的积分，往往适当改变积分路径也可以使得积分可求。

高一次 $x_1,x_2,\cdots,x_q$ $z_1,z_2,\cdots,z_p$ 外处处解析，则积分存在且

\int_{-\infty}^{+\infty}R(x)e^{iax}dx = 2\pi i\sum_{k=1}^p\mathcal{Res}[R(z)e^{iaz},z_k] + \pi i\sum^q_{k=1}\mathcal{Res}[R(z)e^{iaz},x_k]

证明过程略

以上四种方法都是采用了围道积分法，即将实函数的定积分转化为解析函数沿闭合路径的积分，然后运用留数定理转化为留数的计算。

5.4 复变函数奇点类型的判定

5.4.1 奇点类型的判断

首先根据计算极限的方法判断是三种奇点的哪一种。可去奇点的极限有限，本性奇点的极限不存在。大部分情况都是极点。

5.4.2 极点阶数的判断

$z$ $\infty$ 。如判断下面这个函数的极点类型
$\frac{e^z\cdot\sin z}{z^2}$
则有
$\lim_{z\rightarrow0}z\cdot\frac{e^z\cdot\sin z}{z^2} = \lim_{z\rightarrow0}\frac{\sin z}z = 1\ne\infty$
$z$ $\infty$ 了，说明是一阶极点。
利用零点阶数进行判断
前面讲过零点和极点有这样一个关系：
$f(z)$ $z_0$ $\frac1{f(z)}$ $z_0$ 处的m阶极点。
还有一点是分子上的零点阶数或极点阶数可以与分母上的“抵消”，还是上面那个例子。
$e^z\cdot\sin z$ $z^2$ $z^2$ 还有一阶零点。
$z^2$ 在分母，所以分母上有一阶零点，说明整个函数有一阶的极点。所以该函数在0处是一阶极点。

其他类型函数的判断

$z_0$ $\infty$ 不能完全判断是极点还是本性奇点，这点尤其适用与非幂级数构成的函数。

如

e^{\frac z{1-z}}

$z=1$ 时，极限为正无穷，但是不是极点。

因为，如果将函数按照

e^z = \sum_{n=0}^{\infty}\frac{z^n}{n!}

进行展开

e^{\frac z{1-z}} = \sum_{n=0}^{\infty}\frac1{n!}\frac{z^n}{(1-z)^n}

$z=1$ 处的负幂项系数是有无穷多个不为0的，所以是本性奇点。

所以对于不好判断的函数，可以考虑将函数进行泰勒级数展开。

常见的泰勒展开有：

\begin{aligned} &e^z = \sum_{n=0}^{\infty}\frac{z^n}{n!}\\ &\frac1{1-z} = \sum_{n=0}^{\infty}z^n \\ &\sin z = \sum_{n=0}^{\infty}(-1)^n\frac{z^{2n+1}}{(2n+1)!}\\ &\cos z = \sum_{n=0}^{\infty}(-1)^n\frac{z^{2n}}{(2n)!} \end{aligned}

以及这些函数进行加减乘除、微分、积分运算得到的级数展开。

展开便可直接观察负幂项系数的个数，那个才是判断三种奇点类型的根本依据。

无穷远点处奇点的判断

对于无穷远点处的奇点，通常不好直接判断。可令

t = \frac1z

$g(t)$ $t=0$ 处奇点的判断。

如判断下列函数在无穷远点的性质

\frac{z^6}{(z^2-3)^2\cos\frac1{z-2}}

有时候需要进行泰勒级数的展开，如

\frac1{e^z-1}-\frac1z=\frac{z-e^z+1}{(e^z-1)z}=\frac{-\sum_{n=2}^{\infty}\frac{z^n}{n!}}{\sum_{n=1}^{\infty}\frac{z^{n+1}}{n!}} = -\frac12

自变量为函数的复变函数

求下面函数在复平面的奇点

\sin\left[\frac1{\sin\frac1z} \right]

对于这样的复杂的函数，可以令

\omega = \sin\frac1z

$\sin\frac1z$ $z=0$ 一个本性奇点。所以使

\sin\frac1z = 0

$z = \frac1{k\pi}$

原文作者：XiaoQixian

原文链接：http://xiaoqixian.github.io.com/2020/06/23/%E7%95%99%E6%95%B0/

发表日期：June 23rd 2020, 8:35:40 pm

更新日期：June 23rd 2020, 8:35:40 pm

Previous Post

Linux多线程

CATALOG

1. 5. 留数



缺失模块。
1、请确保node版本大于6.2
2、在博客根目录（注意不是archer根目录）执行以下命令：
npm i hexo-generator-json-content --save
3、在根目录_config.yml里添加配置：

jsonContent:
  meta: false
  pages: false
  posts:
    title: true
    date: true
    path: true
    text: false
    raw: false
    content: false
    slug: false
    updated: false
    comments: false
    link: false
    permalink: false
    excerpt: false
    categories: true
    tags: true